Tassi Tamás
Foton és hatáskvantum
Minden az un. fekete-test sugárzással kezdődött. Egy üreges testet hevítve a kis lyukon mindig ugyanolyan karakterű fénysugárzás jött ki, függetlenül az üreg anyagától és színétől. Az energia-görbén volt egy púp, mely két oldalt lecsengett. (Gauss görbe.) Magasabb hőmérsékleten is megmaradt a jellege, bár a púp egyre balrább tolódott és egyre magasabbra került. Nem volt rá magyarázat, hogy a nagy, valamint a kicsiny frekvenciájú fényhullámok miért kapnak egyre kevesebb energiát. Max Planck adta meg a végső magyarázatot 1900 decemberében. Egyre nagyobb frekvenciákon egyre nagyobb a fényhullám energiája, és ezekre egyre kevesebb jut az össz-energiából. Planck képlete az energiára az egyes f frekvenciák függvényében:
EPlanck=h*f
Mindezek után térjünk át a címben szereplő hatáskvantumra. Az össze-vissza pattogó fotonok mindig átveszik az üreg belsejét alkotó atomok energia szintjét. Mire kiérnek, energia-eloszlásuk pontosan leköveti a belső jellemzőket.
A h kvantumállandó, más néven Planck állandó, vagy megint más néven hatáskvantum lényegének közelébe leggyorsabban a mértékegysége útján juthatunk el: kgm2/s. Ebben a furfangos fizikai állandóban rejtetten az m tömeg, a v sebesség és egy r keringési sugár van összeszorozva: m*v*r. Az mvr szorzat szerepe igen jelentős a fizikában. Impulzusmomentumnak, impulzusnyomatéknak vagy perdületnek nevezik, de esetenként hívják forgási-nyomatéknak vagy pálya-nyomatéknak is. A szorzatnak fontos szerepe van a csillagászatban, amennyiben a bolygók keringése során ez egy megbízhatóan megmaradó mennyiség. (Ellentétben a pályasugárral, a sebességgel valamint az impulzussal, mert ezek a keringés során folytonosan változnak.)
Az elemi részecskéknek is van perdülete, azaz impulzusmomentuma. Ezt angol szóval spinnek mondják, és ez is a szubatomi részecskére, valamint a fotonokra jellemző megmaradó mennyiség. Van azonban néhány jelentős különbség az égitestek és az elemi részecskék impulzus-momentuma között. Az égitestek egyszerűen csak megtartották és mindmáig őrzik a keletkezésük időpontjában örökölt perdületet. Nem is tudnák egykönnyen elveszíteni, hiszen az roppant nagy fizikai mennyiség. Ezzel szemben az elemi részecskék impulzusnyomatéka szinte jelentéktelen. Legkisebb és egyben tipikus értéke 53*10-36, ami 75 nagyságrenddel kisebb, mint a Földünké. Valószínűtlen, hogy ez a pici érték értékelhetően hosszú ideig megmarad. Inkább az a helyzet, hogy valami láthatatlan entitás rejtőzik a háttérben,és eme háttér folyamatosan feltölti a részecske impulzus-momentumát az általa megszabott értékre.
Központi égitestünk a Nap. Ez egy hatalmas gázgolyóbis, mely forog a saját tengelye körül. Perdülete óriási, azonban Földünk pálya-momentuma (perdülete) még ennél is 3000-szer nagyobb. Azért ilyen nagy, mert a Föld esetében a perdület mvr képletében nagy a v sebesség és az r sugár értéke. A 3 tagú szorzatban egy 30000 és egy 150 milliárd tag lesz a domináns.
Az elemi részecske sem forog, hanem bolygó módjára kering, és ily módon viszonylag nagy értékű pálya-momentumra tesz szert. A forgási középpontban lehet egy atommag, de lehet, hogy semmi sincs ott. Ilyenkor a vákuum m0 mágneses permeabilitása kényszeríti körmozgásra a szubatomi részecskét. A protonban lévő kvarkok is ilyen kényszer hatására végzik a keringő mozgásukat.
Úgy tűnik, hogy a hatáskvantum a vákuum alapvető fizikai tulajdonsága, és a szubatomi részecskék viselkedését irányítja. Jele h , ami szerencsésen összecseng a magyar hatáskvantum szóval. Bár amint később látni fogjuk legjobb lenne ezt az önállóan nem létező fogalmat elfeledni.
A vákuumnak a h hatáskvantum mellett sok más fontos fizikai jellemzője is van. Ilyen az e0 dielektromos állandó és a m0 mágneses permeabilitás. A vákuum fontosabb adatai tehát:
e0=8,854187817*10–12 C2/Nm2
m0=1,256637061*10–6 Vs/Am
c =299 792 458 m/s
h =662,606 957 417*10−36 Js kgm2/s
S0=52,728 586 290*10-36 Js kgm2/s
 Az eddig tárgyalt fénysugarat időnként részecskének is tekintik és akkor fotonnak nevezik. A fizikai paramétereit – energia, impulzus, spin – elég pontosan ismerik. Közülük a leginkább furcsa mennyiség a spin, melynek értéke kétszerese az általános elemi részecskék spinjének, azaz 2S0. A kétszeres spin okát a mai fizika nem találja. Ezért Jómagam – az ábra szerint – egy olyan foton modellt készítettem, melynél kézenfekvően adódik a 2S0 érték. Az eddig tárgyalt fénysugarat időnként részecskének is tekintik és akkor fotonnak nevezik. A fizikai paramétereit – energia, impulzus, spin – elég pontosan ismerik. Közülük a leginkább furcsa mennyiség a spin, melynek értéke kétszerese az általános elemi részecskék spinjének, azaz 2S0. A kétszeres spin okát a mai fizika nem találja. Ezért Jómagam – az ábra szerint – egy olyan foton modellt készítettem, melynél kézenfekvően adódik a 2S0 érték.
A foton tehát összetett részecske, amely 2 golyóból áll, és ezek egymás körül keringenek. (Semmi közük az elektron – pozitron párhoz, túl nehezek lennének, és elektromos töltésük sincs.) A golyópár fénysebességgel kering egymás körül, és fénysebességgel halad előre. Mindebből mi csak a haladási sebességet észleljük, miközben a golyók térbeli sebessége valójában 1,41c. Végtére is ezt a kettős mozgást a vákuum kényszeríti rá a golyókra, melyek tehát a térben kettős csavarvonalat írnak le. Mivel a golyók egyenként S0 spint kapnak a vákuumtól, az összeg természetszerűleg 2S0-ra adódik.
Ugyanakkor a foton impulzusa kétszeresére adódik, mert pályája miatt a forgás sebessége is haladássá konvertálódik: I=2mc (ahol m a két golyó össztömege)
Ugyanezen megfontolásból, azaz a kettős sebességből eredően a foton energiája 2*2pi*S0. Az első 2-es szám a két darab golyót képviseli, míg a 2 pi a kör kerülete. Ennek r sugara mentén a spin impulzusnyomatéka energiaként jelentkezik, ha az f frekvenciával is beszorozzuk. Amint azt Planck tapasztalti képletként levezette Efoton=h*f. A fenti levezetés logikája szerint viszont a foton energiája Efoton=4pi*S0*f. Ezek szerint a tapasztalatból nyert, és az egyszerűsített számítás maximálisan segítő h hatáskvantum a 4piS0 értéket takarja. A h fogalma és számértéke tehát nem önálló, hanem származtatott entitás. Helyette a spint, és számszerűen az S0=53*10-36 fizikai fogalmat és számot kell használnunk, mert a h önállóan nem létezik:
h = 4piS0
Modellezni is tudjuk a foton fenti ábra szerinti csavarvonal-menti mozgását. A modell alapja egy meredek emelkedésű csavarorsó. Egy menetes anya forog rajta, és a forgásiránytól függően mozog előre vagy hátra. Képviselje a foton tehetetlen tömegét a hengeres palástra kihelyezett 2 darab m/2 tömegű golyó. Megfelelő geometriai arányok esetén ezek mindkét fő irányban v sebességgel rendelkeznek tengely-irányban is, és forgásirányban is. A két golyó mozgási energiája összesen: Emozg=2*m/2(v2/2+v2/2)=2mv2/2. Így tehát a foton ernergiája a képlet rendezése után Emozg=mc2.
Képesek vagyunk arra, hogy a foton furcsa mozgását modellezzük egy technikai eszköz segítségével.
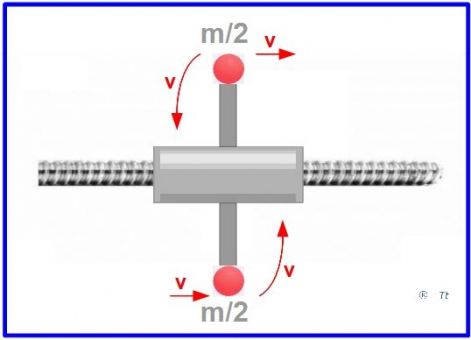
Ez egy meredek emelkedésű csavarorsó. Egy nagyméretű menetes anya forog rajta, és a forgásiránytól függően halad előre vagy hátra. Képviselje tehetetlen tömegét a hengeres palástjára kihelyezett 2 darab m tömegpont. Ezek mindkét fő irányban v sebességgel rendelkeznek tengely-irányban is, és forgásirányban is. Mozgási energiájuk tehát irányonként 2m*v2/2. A két fő irányt összegezve tehát energiájuk 4mv2/2.
Planck hosszú ideig próbálkozott azzal, hogy a hatáskvantumot beillessze a klasszikus fizika kereteibe. Tudjuk, hogy ez a törekvése nem sikerült, "mert a mikrovilágban ettől merőben eltérő törvények érvényesülnek.” – így foglalja össze a hatáskvantum problémáit a mai modern fizika. Ámde amint azt fentebb láttuk, a h megérthető a klasszikus fizika segítségével, és beleillik a klasszikus logika gondolatmenetébe is.
Tassi Tamás
fejlesztőmérnök
aparadox@gmail.hu
Kulcsszavak:
foton, mozgási energia, Planck, hatáskvantum
Ü Főoldal Einstein fellegvára Þ
| 
